Python: Sets

Python Sets

The file system is organized into a hierarchical structure, starting with the root directory

1 Overview

📘 Sets in Python

A set in Python is an unordered collection of unique elements, which means it cannot contain duplicate values. Sets are mutable, allowing for elements to be added or removed, but the elements themselves must be immutable types. Unlike lists or tuples, sets do not support indexing or slicing because they do not maintain any order among their elements.

2 Key characteristics of Python sets include:

• Unordered: The elements are stored without any particular sequence.
• Unique elements: Each element can appear only once in a set.
• Mutable container: The set itself can be modified by adding or removing elements.
• Elements must be hashable (immutable types such as numbers, strings, and tuples).
• Sets support standard mathematical set operations such as union, intersection, difference, and symmetric difference.
• Sets are commonly used for fast membership testing and eliminating duplicates from collections.

Python sets can be created using curly braces {} or the set() constructor, the latter being necessary for creating an empty set. They can be constructed from any iterable, allowing conversion from lists, tuples, or other collections.

Set manipulation methods include adding elements with add(), updating with multiple elements using update(), and removing elements with remove() or discard().

Overall, Python sets provide an efficient and convenient way to work with collections of distinct items with operations resembling those in mathematical set theory.

---

3 Sets

• Unordered collection of unique elements.
• E.g., useful for guaranteeing no duplicates.

---

# Only unique elements are stored, so 2 is only stored once
my_set = {1, 4, 2, 3, 2, 2}
print(my_set)

{1, 2, 3, 4}

---

4 Indexing Not Allowed

• Set elements are unordered, so we cannot access them using indices:

my_set = {1, 4, 2, 3, 2, 2}
print(my_set[1])

TypeError: ‘set’ object is not subscriptable

---

5 Mutability

• sets are mutable.
• To add elements to a set, use add() method.

my_set = {1, 2, 2}
my_set.add(5)
print(my_set)

my_set = {1, 2, 5}

---

• To remove elements, use remove() method.

my_set = {1, 2, 5}
my_set.remove(2)
print(my_set)

my_set = {1, 5}

---

• Multi-type:

my_multi_set = {'apple', 1, 2.5, True}

---

• However, only immutable types are allowed inside sets!

print({'apple', 1, 2.5, [1, 2]})

TypeError: unhashable type: ‘list’

print({'apple', 1, 2.5, True, (1, 2)})

{(1, 2), 1, 2.5, ‘apple’}

---

• Convert sets to lists or tuples and vice versa.
• Take care: repeated elements from the list are removed when converting to a set.

list2set = set([1, 2, 3, 3, 3])
print(list2set)

set2list = list({1, 2, 3})
print(set2list)

{1, 2, 3}
[1, 2, 3]

---

tuple2set = set((1, 2, 3, 3, 3))
print(tuple2set)

set2tuple = tuple({1, 2, 3})
print(set2tuple)

{1, 2, 3}
(1, 2, 3)

---

6 in

• Like lists, check if an element is inside a set:

print(3 in {1, 3, 2})

True

print(5 in {1, 3, 2})

False

---

7 Operations

From: https://www.learnbyexample.org/python-set/

---

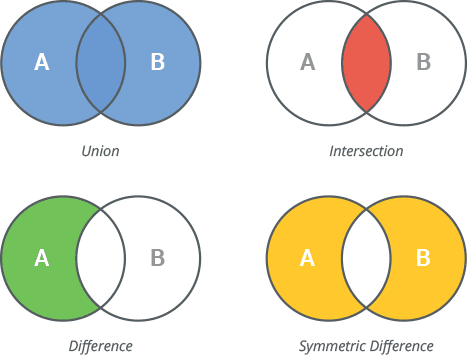
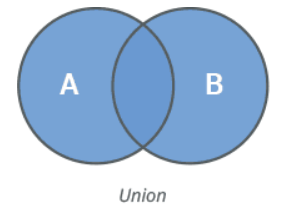
8 Union

• With | or union().

set1 = {1, 2, 3}
set2 = {3, 4, 5}

# Union
union_result = set1 | set2
# or
union_result = set1.union(set2)
print(f'The union is: {union_result}')

The union is: {1, 2, 3, 4, 5}

Union operation in python

From: https://www.learnbyexample.org/

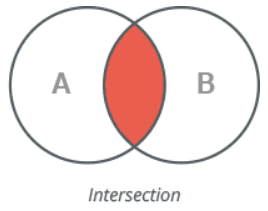
9 Intersection

• With & or intersection().

set1 = {1, 2, 3}
set2 = {3, 4, 5}

# Intersection
intersection_result = set1 & set2

# or
intersection_result = set1.intersection(set2)

print(f'The intersection is: {intersection_result}')

The intersection is: 3

Intersection operation in python

From: https://www.learnbyexample.org/

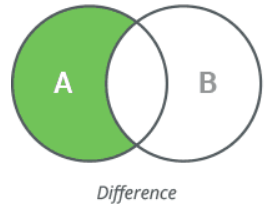
10 Difference

• With - or difference().

set1 = {1, 2, 3}
set2 = {3, 4, 5}

# Difference
difference_result = set1 - set2

# or
difference_result = set1.difference(set2)

print(f'The difference is: {difference_result}')

The difference is: {1, 2}

Difference operation in python

From: https://www.learnbyexample.org/

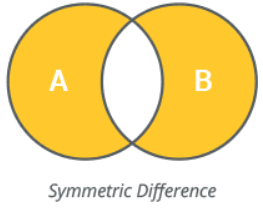
11 Symmetric difference

• With ^ or symmetric_difference().

set1 = {1, 2, 3}
set2 = {3, 4, 5}

# Symmetric Difference
symmetric_difference_result = set1 ^ set2

# or
symmetric_difference_result = set1.symmetric_difference(set2)

print(f'The symmetric difference is: {symmetric_difference_result}')

The symmetric difference is: {1, 2, 4, 5}

Symmetric difference operation in python

From: https://www.learnbyexample.org/

12 Functions and methods

• Common built-in functions: len(), sum(), max(), etc.

set1 = {1, 2, 3}

print(f'The length of my_set is {len(set1)}.')
print(f'The sum of my_set is {sum(set1)}.')
print(f'The max of my_set is {max(set1)}.')

The length of my_set is 3.
The sum of my_set is 6.
The max of my_set is 3.

---

• Other common methods: issubset(), issuperset().

set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {3, 5}

print(f'Is set3 a subset of set1? {set3.issubset(set1)}')
print(f'Is set3 a subset of set2? {set3.issubset(set2)}')
print(f'Is set2 a superset of set3? {set2.issuperset(set3)}')

Is set3 a subset of set1? False
Is set3 a subset of set2? True
Is set2 a superset of set3? True

---

• More methods: https://www.w3schools.com/python/python_ref_set.asp.

---

13 Update

# Update set1 with the union of set1 and set2.
# This modifies the content of set1.

set1.update(set2)
print(set1)

{1, 2, 3, 4, 5}

---

14 Iteration

• The same as lists and tuples:

for element in {1, 2, 3}:
    print(element)

1
2
3

---

15 Comprehension

• Similar to lists:

even_set = {i * 2 for i in range(5)}
print(even_set)

{0, 2, 4, 6, 8}

---

16 Example

Given a string, count the number of distinct words present in the string.

text = "one two three three two one go"

unique_words = set(text.split())
distinct_words = len(unique_words)

print(unique_words)
print(distinct_words)

{‘two’, ‘go’, ‘three’, ‘one’}
4

---

17 Exercises

17.1 Set operations

Given two sets, you can perform various operations to analyze their relationships. Each operation provides different insights into how the sets relate to one another. Given two sets, display their:

• Union combines all unique elements from both sets.
• Intersection finds elements that are present in both sets.
• Difference identifies elements that are in the first set but not in the second.
• Symmetric Difference includes elements that are in either of the sets but not in both.

Example 1

Input: set1 = {1, 2, 3, 4, 5}, set2 = {4, 5, 6, 7, 8}
Output: Union: {1, 2, 3, 4, 5, 6, 7, 8}
Intersection: {4, 5}
Difference: {1, 2, 3}
Symmetric Difference: {1, 2, 3, 6, 7, 8}

Example 2

Input: set1 = {10, 20, 30}, set2 = {30, 40, 50}
Output: Union: {10, 20, 30, 40, 50}
Intersection: {30}
Difference: {10, 20}
Symmetric Difference: {10, 20, 40, 50}

Example 3

Input: set1 = {1, 2}, set2 = {1, 2}
Output: Union: {1, 2}
Intersection: {1, 2}
Difference: set()
Symmetric Difference: set()

17.2 Membership

Given a set of integers and an element, check if the specified element is present in the set.

Example 1

Input: my_set = {1, 2, 3, 4, 5}
Input: element = 3
Output: True

Example 2

Input: my_set = {1, 2, 3, 4, 5}
Input: element = 6
Output: False

Example 3

Input: my_set = {‘apple’, ‘banana’, ‘cherry’}
Input: element = ‘banana’
Output: True

17.3 Sub and superset

Given two sets, determine if the first set is a subset of the second set, and simultaneously check if the second set is a superset of the first set. A set is considered a subset of another set if all elements of the first set are contained within the second set. Conversely, a set is a superset of another set if it contains all elements of the first set.

Example 1

Input: set1 = {1, 2, 3}
set2 = {1, 2, 3, 4, 5}
Output: Set1 is a subset of Set2: True
Output: Set2 is a superset of Set1: True

Example 2

Input: set1 = {1, 2, 6}
set2 = {1, 2, 3, 4, 5}
Output: Set1 is a subset of Set2: False
Output: Set2 is a superset of Set1: False

17.4 Unique elements

Given a list of elements, the task is to create a new list that contains only the unique elements from the original list. Use the set data structure to easily solve this problem.

Example 1

Input: my_list = [1, 2, 3, 2, 1, 4, 4, 5]
Output: [1, 2, 3, 4, 5]

Example 2

Input: my_list = ['apple', 'banana', 'apple', 'orange', 'banana']
Output: ['apple', 'banana', 'orange']

Example 3

Input: my_list = [True, False, True, True]
Output: [True, False]

17.5 Attendance

You have attendance lists for 3 different courses. Find students who assisted all classes.

Example

Input:
math = [“Alice”, “Bob”, “Charlie”, “John”, “Eve”, “Abbott”]
physics = [“Bob”, “Eve”, “Charlie”, “David”, “Alice”, “Susan”]
cs = [“Charlie”, “Abbott”, “Bob”, “David”, “Eve”]
Output: {‘Charlie’, ‘Eve’, ‘Bob’}

17.6 Disjoint sets

Given two sets, determine if they are disjoint, meaning they have no elements in common.

Example 1

Input: set1 = {1, 2, 3}
set2 = {4, 5, 6}
Output: Set1 and Set2 are disjoint: True

Example 2

Input: set1 = {1, 2, 3}
set2 = {3, 4, 5}
Output: Set1 and Set2 are disjoint: False

Example 3

Input: set1 = {'a', 'b', 'c'}
set2 = {'d', 'e', 'f'}
Output: Set1 and Set2 are disjoint: True

Example 4

Input: set1 = {1, 2, 3}
set2 = {2, 3, 4}
Output: Set1 and Set2 are disjoint: False

17.7 Missing Numbers

You’re given an integer n and a list of numbers that should contain all elements from 0 to n, in no specific order. However, some values have been lost. Display the missing elements in ascending order.

Example

Input: n = 10; rng = [4, 8, 2, 1, 3, 9]
Output: [0, 5, 6, 7, 10]